
Disentangling the data of hyperfunctional everyday technology
LEGAL DISCLAIMER: In order to preserve the Intellectual Property (IP), the overall presentation of the research details for the physico-mathematical analysis to disentangling the data hyperfunctional everyday technology is not included. Only fragments that are structurally the same are presented, on the basis of which the research-scientific procedural modelling steps could be comprehended in a plausible way. Nevertheless, this sketch is subject to copyright protection too. IP infringements are sanctioned in accordance with § 106 Copyright Act (UrhG) Section 78 para. 3 no. 4 German Criminal Code (StGB).
Preamble
Linguistic confusion: generally known as the divine sanction against progressive disinhibition in the scriptural city of Babylon. It is irrelevant whether this communication chaos was Yahweh’s punishment for human presumptuousness or whether it is because, in times of yore, we surrendered to the loss of control and understandability of language. It is, however, a daunting parallelism to our modern vulnerability of becoming estranged from our own overflowing catalog of inventions. Our profound dependence on these inventions, which even affects the fate of our planet, makes it necessary to disentangle the data of hyperfunctional everyday technology.
[…The remains of the »Tower of Babel« are barely discernible today. Legend has it that about two thousand years later, Alexander the Great had the imperial temple grounds demolished, reducing them to a quarry for centuries. A smelly swamped hallow is the only remainder of the Tower of Babel …].
Therefore, it was neither wars nor natural disasters that extinguished said civilized "prehistoric modernity", but the communication chaos that arose from it. This communication chaos arose from the gigantic variety of dependency-promoting inventions (similar to our modern-day situation) that has become impossible to keep track of, as the indispensable control and understandability of such was or is being neglected
The political, financial, and industrial caprioles of the market and the chaotic overbidding of innovative ideas to solve our global problems reflect the loss of control of science and research over this mass. In this regard, FEAT will initiate the intentional harmonization of terminology. The plethora of at times outlandish, often incomprehensible terms will be re-cataloged with rational interpretation. To do so, they will condensate the properties shared by functional everyday technology as far as possible to a common denominator. This common denominator designates the function of the technology as straightforward and understandable for the end user as possible. While companies see themselves forced to create their own terminology, FEAT will act as the harmonizing interface that will move away from expansional vocabulary to an intentional one that will streamline production, research and innovation. Of course, from an algorithmic perspective, a mathematics-based process to transfer information with matrix-vector multiplications can attain this goal.
By way of explanation: Day and night, virtually 4 billion Internet users from all around the globe clutter the server centers with a sometimes-unfiltered concoction of often absolutely spontaneous trains of thought and sentimentalities that require most precise algorithmic recording and categorization before even arriving at their intended addressees in only a fraction of a second! Meanwhile, however, the flood of information from these technologies have formed a chaotic collective of data that can only the aforementioned »algorithmic treatment plant« can disentangle and purify. The following serves as a clarification of my thoughts concerning the intercommunicative "disentanglement of hyperfunctional everyday technology" as a necessary attribute for our research goals.
As an introduction:
Based on "Moore's Law", the computational power of any given personal computer doubles at least every 1 1/2 years. However, as the needed computational power already overly exceeds the planned capacity of that algorithmically automated PC brain (processor), the large computer manufacturers had no other choice - at the latest after Nine Eleven- to integrate an ever-increasing number of such processors in one PC that need to process information and compute at the same time.
A comparison to illustrate this further: let's presume that a Dr. Sciencefiction would start to transplant more and more parallel brains or brains working in parallel into our already chronically overburdened heads. Result: The person is pushed over the edge and... perishes! However, since we increasingly transfer our mental effort to such "surrogate brains" (computers) - in other words, we happily "outsource" the work, such overstrain and overstepping of physical limitations ultimately led to trying to "square the circle".
If then, here at my small workstation computer, I endeavor to ponder about intercommunicative data disentanglement of hyperfunctional everyday technology, I can assume that in my PC there is a manageable number of processors (cores, known as dual-core, quad-core) working in parallel. The case is quite different in 'supercomputers' as they are used in banks, clinics, research companies, large corporations, etc. on a daily basis. Such large computers have an almost ridiculously large amount of processors, that it is child's play for hackers to find security gaps through which they can access highly sensitive data. This can be compared to an overworked human brain, which is naturally much more easier to manipulate than a cool head.
For example, the Marburg cluster MaRC currently encompasses about 600 computer cores while the clusters operated by secret services have crammed more than a quarter million of such parallel processors into a confined space. This gigantic swell in power, however, is partially attributable to an ever more granular and sophisticated level of virtualization of basically very analog daily tasks: market research, market analysis, market decisions, opinion polls, tectonic movement monitoring, weather forecasts, climate modeling, earth warming simulations, multimarketing, money transfers of all kind - a true cyber-frenzy - terrorist identification and counterterrorism, etc.... the list of the most varied plethora of data and information transactions ins never-ending.
Last but not least, consider the almosty 4 billion Internet users from all around the globe who clutter the server centers with completely unfiltered connection of, often most, completely spontaneous trains of thought and sentimentalities that need to be algorithmically recorded and categorized with the highest precision before even arriving at their intended addressees in only a fraction of a second!
It is high time that entirely new algorithms be developed; algorithms which FEAT wants to help create and apply: As a starting point, we will take the equation n = md for m = 4 in the graph below:

As for the aforementioned reasons we basically only work with parallel processors nowadays, their nominal power barely translates to their real performance. While the manufacturer may indicate a "performance guarantee" of sorts with the calculated peak performance, in reality this superlative is usually unattainable, because he pretends that the computer can output all individual performances to their maximum at the same time. That means that the manufacturer simply adds up all individual performances, as if the performance was achieved with a series of individual computers - but common knowledge dictates that this is complete nonsense if not an outright lie.
By way of elucidation: multitasking requires even more processing power for algorithmic coordination and to dovetail completely different performance requirements in the same computer. Let us picture a highly simplified model of the inside workings of a computer: The computer, as originally designed, is made up of a central processing unit (CPU) and a storage unit - without considering input and output components. All data to be processed are in the storage unit, including the computer program doing the processing itself. Moreover, the CPU has a central clock to structure the individual processing steps. On the one hand, a CPU can always only issue and execute one program instruction at a time, although it is unquestionable that it can also use several clock cycles at the same time.

Here (in this primordial computer), the CPU operated with only a little amount of data and smaller local storage units, known as registers, as well as data bundles from a main storage unit. Meanwhile, the access to the storage units is also clocked, albeit with a longer seek time. However, as each signal within a given cycle has to reach the CPU in full, even the speed of light acts as a "physical impediment" (always in correlation to the size of the respective chip).
Currently, the normal cycle time of an ordinary PC processor is of about 2 GHz. In other words: a single processing command takes a full 0.5 nanoseconds to complete, that is: a five-hundred-thousand-billionth of a second. While light can travel around the Earth seven times in one second, billions and billions of such cycles are completed in the same amount of time all over the world. To summarize: The challenge of the need of increased performance was answered with quantity instead of with quality:
In practice, both resources, the storage unit and the CPU are considered equal and are to be used to the same extent, it is the CPU of all things, that is, the "gas pedal" of the data vehicle, that turns out to be the "brake" as it acts as a bottleneck that is permanently "constipated" due to the amount of data it has to process. The unequal distribution of the load thus calls for a corrective action in the algorithmic architecture of the computer. This can be compared to a human being who likes to multitask intensively, thereby risking burnout. The parallels that can be drawn between the human brain and computer processors in regard to performance overstraining are striking.
However, this bottleneck can be prevented: Difficult tasks are subdivided to manysmaller tasks, thus speeding up the processes and reliving the processors of some of the strain. However, instead of resorting to coordinating the tasks by means of algorithms, it is blatantly evident that both convenience and the avaricious competitiveness of the manufacturer are to blame for the fact that this excessive load of global data processing, which has long since gotten out of hand, has been counteracted with the moronic "cloning" of additional parallel processors creating a gigantic pool filled with a chaos of information data, the only remedy for which is to use a mathematic ordering process that acts as some sort of algorithmic purification plant to detoxify and disentangle it. See fig. cloning methods used:

To clarify: our working computers usually have a shared random-access memory. In view of lacking CPU power, the individual processors constantly compete for access to this RAM. That means that the processors themselves are on a chip of their own as what has been termed as "cores" (dual core, quad core). It is here where all processor data can be accessed - and this is precisely the problem! While it is possible to solve individual coordination problems with regards to multiple access to data with expensive additional hardware, their developed algorithms will usually concentrate on intense parallelization or streamlining of the individual tasks. This "trick", however, only works to a certain, manageable extent.
In comparison: a person who has to manage several projects at the same time can often only do so with the help of stimulants. In using such expensive additional hardware to increase performance, the processors "wear out" much faster as well. Here as well it is possible to draw a parallel between the peculiarities of our own human intellectual muscle and our, so to speak, "surrogate" brain of our invention, the computer.
In computer technology jargon, these hardware additions are also known as multiprocessor systems.
If several processors are used, each processor has a storage unit of its own (distributed system see. fig.). The Marburg cluster (MaRC) mentioned earlier in this text, for example, has 140 quad core processors. However, as this architecture places enormous performance demands on the network connecting the processors, not only the work or individual tasks but also the data has to be distributed among several processors because of the indulgence in parallel algorithms.
Just imagine: Units supposed to deliver performance are misused as data storage devices because the excessive data is simply assumed to be important, as if every bit of it was the carrier of unique, exceptionally vital information. By literally "clogging up" these important units with an excess of information, mostly made up of disposable data, using obtuse parallel algorithms, more and more parallel processors will be needed on the long term. Snow ball effect!
Basically, this architecture also corresponds to the system variant "Internet", which, however, is a greater convolution of spam caused by quantum processing with parallel-algorithmic methods, meaning that focus is put on quantity instead of quality. Added to this, there is an entire plethora of other problems, for example the fact that billions of Internet users use a variety of different operation systems with an equal variety of data transfer capabilities - which ultimately exacerbates the development of algorithms suitable for the challenge.
An ad-hoc solution would be to retrofit modern computers in the sense that every access to the storage unit slows down the cycle time of the CPU and every processor P see fig. below would have a smaller cache storage unit C fig. in addition to its central processing unit R. The processor could then access this additional unit considerably faster than if it could only access the main memory. This would at least free the overburdened processors from clumps of superfluous data, at least on the short term.

In practice, you'd be able to buffer some of the data retrieved from the main memory P in cache C to immediately continue using it if needed later on, provided that and as long as this data was not pushed out by new incoming data as the storage capability of cache C is small. There is a hierarchical cache system with which it is possible to use the algorithms from linear algebra, for example matrix vector multiplication, to create efficiency differences depending on whether the cache can hold the totality of all data that is being processed at a given time. If it can't, this data would have to be reloaded several times, which is a time-consuming process (cache fault). This precise problem can be prevented with matrix/vector allocation in smaller data packages.
A trivial handicap in the conventional approach to algorithm development is the not uncommon dependence on interim results by standardized processes, that is, processes that do not cater to any specific need. In other words, the parallel algorithm on the one hand generates a standardized data processing method while on the other hand much of this data is far too different from one another that they could be processed by standardized means. This combination of data distortion and data misdirection creates those time and energy consuming dependencies that express themselves as data channel bottlenecks. Such parallelization can, for example, be prevented with linear recursion:(ai,bi ∈R)wherex1:=a1andxi:=bixi−1+ai,i=2,...,n.
Explanation of the formula: bi ≡1 is initially represented by a simple sum. It is further suggested that xn can only be calculated if xn−1 is known. In consequence, this would imply an expenditure of n time units (which, after taking a closer look, is not the case). In truth this enables a calculation in time units of log2 n, provided n processors are being used. Based on these previous results x2 = a2 + b2a1, x3 = a3 + b3a2 + b3b2a1, x4 = a4 + b4a3 + b4b3a2 + b4b3b2a1 the following general conclusion can be made:
This interim formula is based on the recursive doubling method, according to which n = 8 = 23 . Ultimately, the result x8 can also be derived from:
x8 = (a8 + b8a7) + (b8b7)(a6 + b6a5) + (b8b7)(b6b5)(a4 + b4a3) + (b4b3)(a2 + b2a1)).
With p = 7 processors it would be able to calculate in steps of 3 = log2 8, however subject to the simplified premise that only one multiplication (axpy operation) can be carried out per step as follows: y := ax + y. While, in general, a computer simply overwrites or glosses over these variables, the relevant interim results have been identified here with apostrophes:

This procedure of solution is therefore in correlation with the upstream, or respectively downstream, brackets:

This simple example already shows the typical characteristics of parallel algorithms:
-
A sequential recursion requires n-1 axpy operations, recursive doubling, however, twice as many.
Therefore, the parallel algorithm requires a significantly higher runtime that the sequential algorithm itself.
2. If, alternatively, one had a considerable larger amount of processors available, reducing runtime to below
would still not be possible, as even this algorithm is always limited by its own degree of parallelization.
3. While in step 1 all 7 processed needed were used, in step 2 only three are left, allowing to calculate the final result with only one processor. Here the unpropitious distribution of the respective loads becomes, once more, apparent.
All 3 issues appear on a regular basis in the context of more extensive problems and are responsible for the fact that when using p processors, the multiple of 1/p of the original runtime will never be necessary. What a waste of time and energy! The following fundamental ideas have been worked out in further detail using advanced matrix vector multiplications (s. formula) →
in treatises that analyze this in more depth. If necessary, supplementary information packages are added, provided that their applicability correlates with the intelligibility of the one using them. That means that always, and only if, the guiding principle of the company that benefits from our research results are in line with the goals for the common good of FEAT, the practical solutions of our scientific research work will be made available.


See below an arbitrary numerical example with simplified analog graphics:





Explanation:
From the point of view of the periodic functions sine and cosine, the most natural number is not 1 but 2π because it holds: 1) sin(x + 2π) = sin(x) || 2) cos(x + 2π) = cos(x). For all real numbers x and 2π, however, is the smallest number of this property. We call them the period (or period length) of the sine and cosine functions. See diagrams of the 2 functions, relating to each other through a simple relationship: cos(x) = sin(x + π/2). In that sense, they are just "shifted" versions of each other. If the variable “x” has the meaning of time (or a quantity that is proportional to time) traversing uniformly from left to right in the above diagram, the

behavior of the function values describes a regular, i.e. harmonic up and down, between the values –1 and +1. Twice as fast operations are described by the functions sin (2x) and cos (2x), three times as fast operations by the functions sin (3x) and cos (3x), etc.
For this we choose the function which is constant 1. All these functions together are the trigonometric basis functions for period 2π. Let's summarize: A) 1 (constant function), B) cos(nx) for n = 1, 2, 3, ... C) sin(nx) for n = 1, 2, 3, ... The constant function 1 belongs in a certain way to the group of cosine functions, since we can regard it as a special case of cos (nx) with n = 0 (remember, that cos (0) = 1). For the functions sin (nx), however, we would only get the constant function 0 with n = 0. [See the next diagrams]:

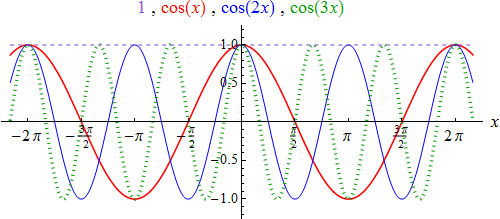
The graphs of the functions sin (nx) and cos (nx) for n > 1 are obtained from those of sin (x)|cos (x) by corresponding "upsets" in the “x”-direction. If we think of x as time, then match:
sin (x) and cos (x) of the fundamental of a system (with period 2π),
sin (2x) and cos (2x) of the first harmonic (they have the period π and hence the period 2π),
sin(3x) and cos (3x) of the second harmonic (they have the period 2π/3 and hence the period 2π), etc.
Although the higher basis functions have smaller period lengths than sin (x) and cos (x) – and the constant function 1 has each number as period length – but in the following considerations we always use 2π as the base period to which we refer: considering each interval, the length of which coincides with period 2π, there is the same amount of surface area as above the x-axis.
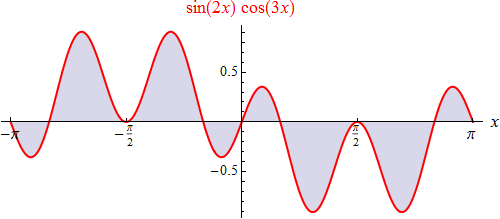
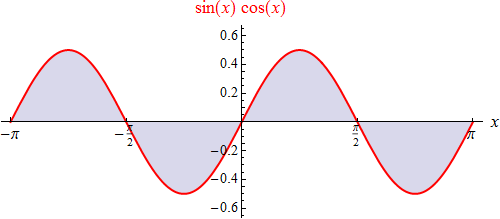
Since the specific integral measures the oriented surface area between graph & x-axis (ie evaluates surface areas below x-axis negatively), it’s obvious that {c + 2π /∫ sin (x) cos (x) dx/c} = 0, regardless of which value is assumed for the lower c-limit. Usually, in such expressions, the interval is chosen to be symmetrical with respect to the zero point, ie c = –π is set, whereby this shape will be accepted: {π/∫ sin (x) cos (x) dx/– π} = 0. We could do the same with any 2 of 4 basic functions as long as they are different: for example, the graph of the product sin (2x) cos (3x) looks like this one on the left.
In the following we consider the “sawtooth function” defined in our base interval by f(x) = x für –π < x < π and is periodically continued on all ℝ…see this graph:
It’s discontinuous for all odd multiples of π. Since it’s an antisymmetric function, a0=0 and an=0 for n=1, 2, 3, … So, we only calculate the evolution coefficients bn: bn= 1/π * {π / ∫ x sin(nx) dx/– π} = –[2 (–1)n/n].

Only in the vicinity of the points of discontinuity, there is still some restlessness that does not correspond to the course of the sawtooth function. By adding more terms, we can push them together, but not completely get rid of them, as long as we only work with finite rows. In short: the series then converges everywhere except at the points of discontinuity against the given function.

From this formula we take the values of the first 4 coefficients b1 = 2, b2 = –1, b3 = 2/3 and b4 = –1/2. The trigonometric polynomial (“g4”) consisting of the corresponding four terms already approximates the “sawtooth function” in a recognizable manner, although not precisely. (See graph on the left). The trigonometric polynomial g10, which consists of the first 10 terms, is already approaching the sawtooth function as seen here:
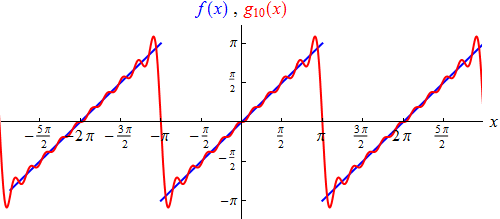

Finally: the next / last graph is continuous in every point, but not differentiable at any point. For example, based on these simplified visualizations, an IT frequency – created by FEAT – would be formulated as follows:
At the points of discontinuity it converges – as already mentioned above – to the mean value of left-sided and right-sided limit of the given function, ie against the value 0. The graph of the function represented g∞ thus looks like the next graph. This agrees with that of the sawtooth function except at the points of discontinuity where we have not fixed it.
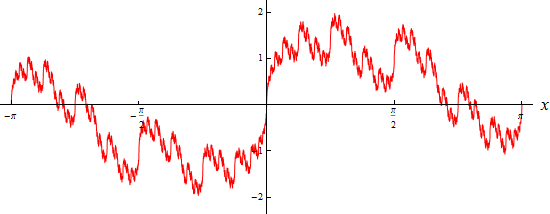

The following arbitrarily outlined graphics illustrate some of our usable IT inter-frequencies from a different perspective. The. compatibility linebetween existing and new inter-frequency runs exactly through the "middle":





Overall, the following is stated: By virtue of this new log-integral algorithm, the performance capacity of the individual computer increases immensely. At the same time, this new frequency key ensures completely hacker-resistant security by means of a 2-fold or even x-fold component encryption (+ op. cit. “compatibility line”). For reasons of know-how protection, only hints are given here without having to disclose the top-secret formulas.
Courtesy of: © LP, 03/12/2019



